哥德巴赫猜想不能用初等方法证明吗?
中文摘要:哥德巴赫猜想这道200多年的数学难题,至今数学家尚未能证明。有的数学家
说:哥德巴赫猜想不可能用初等方法得到证明,并且断言:除非世界一流数学家,否则无法求证。但是,著名数学家华罗庚曾经有言;“神奇易化是坦道,易化神奇不足提,”受此启发和恰逢偶然机遇,作者自不量力从1978初开始探索这颗让数学家梦寐以求的“数学皇冠上的明珠”迷藏之所在。
说:哥德巴赫猜想不可能用初等方法得到证明,并且断言:除非世界一流数学家,否则无法求证。但是,著名数学家华罗庚曾经有言;“神奇易化是坦道,易化神奇不足提,”受此启发和恰逢偶然机遇,作者自不量力从1978初开始探索这颗让数学家梦寐以求的“数学皇冠上的明珠”迷藏之所在。
第一步:转化命题.把哥德巴赫猜想的A命题(不小于6的每一个偶数都能表示成2个奇素数之和)转化成为:不小于8的每一个偶数前边的区间都有对称存在的素数(A ′)。
第二步:找出素数的分布规律。
第三步:创造一个预备定理。定理的证明方法是科学归纳法。
第四步:用预备定理证明转化命题。因为A Û A′,所以就证明了哥德巴赫猜想。
关键词:转化命题 预备定理 著名数学家华罗庚说过:“神奇化易是坦道,易化神奇不足提。”但是有的专家却认为哥德巴赫猜想不可能用初等方法证明,至少在最近几十年内不可能用初等方法证明.那么,如果说真的有谁已经用初等方法证明了哥德巴赫猜想,大概会有人认为这是“痴人说梦”吧?
居里夫人曾经说过:“生活就是一个科学的梦。”所以生活中发生的事往往和人们所预想的大不相同。
下面简介一种用初等数学方法如何证明哥德巴赫猜想。
第一步:把哥德巴赫猜想的(A)命题(不小于6的每一个偶数都能表示成2个奇素数
之和)转化为:不小于8的每个偶数前边区间都有对称存在的素数(A ′)。
居里夫人曾经说过:“生活就是一个科学的梦。”所以生活中发生的事往往和人们所预想的大不相同。
下面简介一种用初等数学方法如何证明哥德巴赫猜想。
第一步:把哥德巴赫猜想的(A)命题(不小于6的每一个偶数都能表示成2个奇素数
之和)转化为:不小于8的每个偶数前边区间都有对称存在的素数(A ′)。
(A) 命题和(A′)命题是否像2×2=4那样完全相等呢?即是否有A A′这种关
系呢?
其实这是很显然的,因为8以后的每个偶数都是它前边区间里二个对称位置上的数
之和,所以,如果不小于6的每个偶数都能表示成二个奇数之和(A)成立的话,也就是
说在不小于8的每个偶数前边的区间内都有在对称的位置上存在着的奇素数。如:
系呢?
其实这是很显然的,因为8以后的每个偶数都是它前边区间里二个对称位置上的数
之和,所以,如果不小于6的每个偶数都能表示成二个奇数之和(A)成立的话,也就是
说在不小于8的每个偶数前边的区间内都有在对称的位置上存在着的奇素数。如:
1、2、3、4、5、6、7、8、9、10、11、12、…… 、n.
8=1+7=2+6=3+5:
10=1+9=2+8=3+7=4+6:
12=1+11=2+10=3+9=4+8=5+7:
8=1+7=2+6=3+5:
10=1+9=2+8=3+7=4+6:
12=1+11=2+10=3+9=4+8=5+7:
┆.
2n=1+(2n-1)=2+(2n-2)=…=p1+p2=(n-1)+(n+1)
(A) 命题中包括6,为什么不从6开始呢?因为6只能写成6=3+3,是两个相同的素数
2n=1+(2n-1)=2+(2n-2)=…=p1+p2=(n-1)+(n+1)
(A) 命题中包括6,为什么不从6开始呢?因为6只能写成6=3+3,是两个相同的素数
而从对称位置上看,3是偶数6前边区间的对称中心,所以把6舍弃。
于是若不小于8的每个偶数都能表示成二个奇素数之和,则这二个奇素数一定是在对称的位置上存在着,这是显而见的,即A A′。
第二步:找出素数的分布规律。
我们知道,可以把自然数分成:单位数、素数、合数。单位数就是1,因为它既不是素 数也不是合数,把它舍弃不写,从2开始写出自然数的序列:
2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、…、n
素数都坐落在哪些位置上呢?也就是说它们的分布规律是什么呢?看来是“一稀二
乱”。其实是很有条理,确有规律的,而且这条规律说来却是这样简单:每轮间隔本位数减一(i – 1)逐次勾掉一些数,则余下的数全是素数。如:
当本位数(i)是2时,2-1=1,即对于2来说每次间隔一个数勾掉一些数,很显然,勾掉 的数都是包含2这个因子的合数:当本位数(i)是3时,3-1=2,即对于3来说,每次间隔二个数勾掉一些数,很显然,勾掉的数都是包含3这个因子的合数:余此类推,即把n以内的所有合数全都勾掉了,余下的当然全是素数.勾掉的结果如下面所示:
2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、.. .n。
第三步:创造一个预备定理。定理的命题是:
在直线方向上有带自然编号的(等距)点n个,如每轮间隔点乘2(i×2),逐次勾掉一些点,则在余下的点中仍有对称点存在(LP)。
因为所说的是对称点,所以n最小是2,即n≥2,n可以为任意大的数.但不是无穷大。显然在没勾掉一些点之前,1号点和n号点对称;2号点和(n-1)号点对称;如此等等。但若按上述给定的规则勾掉一些点后,就不一定还有对称点存在了。这就需要证明。命题证明以后才能成为定理。那么如何证明呢?看来也不是那么容易的。但是你若懂得一点逻辑学,那怕只懂得科学归纳法,就能毫不费难地把它证明出来。科学归纳法有如下的公式;
于是若不小于8的每个偶数都能表示成二个奇素数之和,则这二个奇素数一定是在对称的位置上存在着,这是显而见的,即A A′。
第二步:找出素数的分布规律。
我们知道,可以把自然数分成:单位数、素数、合数。单位数就是1,因为它既不是素 数也不是合数,把它舍弃不写,从2开始写出自然数的序列:
2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、…、n
素数都坐落在哪些位置上呢?也就是说它们的分布规律是什么呢?看来是“一稀二
乱”。其实是很有条理,确有规律的,而且这条规律说来却是这样简单:每轮间隔本位数减一(i – 1)逐次勾掉一些数,则余下的数全是素数。如:
当本位数(i)是2时,2-1=1,即对于2来说每次间隔一个数勾掉一些数,很显然,勾掉 的数都是包含2这个因子的合数:当本位数(i)是3时,3-1=2,即对于3来说,每次间隔二个数勾掉一些数,很显然,勾掉的数都是包含3这个因子的合数:余此类推,即把n以内的所有合数全都勾掉了,余下的当然全是素数.勾掉的结果如下面所示:
2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、.. .n。
第三步:创造一个预备定理。定理的命题是:
在直线方向上有带自然编号的(等距)点n个,如每轮间隔点乘2(i×2),逐次勾掉一些点,则在余下的点中仍有对称点存在(LP)。
因为所说的是对称点,所以n最小是2,即n≥2,n可以为任意大的数.但不是无穷大。显然在没勾掉一些点之前,1号点和n号点对称;2号点和(n-1)号点对称;如此等等。但若按上述给定的规则勾掉一些点后,就不一定还有对称点存在了。这就需要证明。命题证明以后才能成为定理。那么如何证明呢?看来也不是那么容易的。但是你若懂得一点逻辑学,那怕只懂得科学归纳法,就能毫不费难地把它证明出来。科学归纳法有如下的公式;
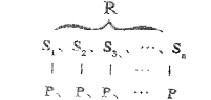
其中S1、S2、S3、…、Sn是我们研究的对象;R是加给诸对象的原因;P是结果。
当我们加给诸对象相同的原因R时,必然得出相同的结果P来。我们观察S1、S2、S3以至更多一些,在R的作用下都有结果P,于是就可以推断Sn有结果P。
据此,我们就能很容易地证明预备定里(LP)。因为我们加给直线方向上的(等距)点的原因R是:每轮间隔点号乘2(i×2)逐次勾掉一些点。然后观察二个点时,三个点时,四个点时,以至更多一些点时,仍有对称点存在,所以即可推知n无论为多么大的数时仍有对称点存在。
也许有人不承不认这种证明,或者不满意这种证明。那么是否能找到一种具有数学表现形式的证明呢?回答是肯定的。因限于本文篇幅和目的,具有数学表现形式的证明从略。
第四步:用预备定理(LP)证明(A′)命题。
在点的序列下一一对应着写上从3开始的奇数列,如图:
当我们加给诸对象相同的原因R时,必然得出相同的结果P来。我们观察S1、S2、S3以至更多一些,在R的作用下都有结果P,于是就可以推断Sn有结果P。
据此,我们就能很容易地证明预备定里(LP)。因为我们加给直线方向上的(等距)点的原因R是:每轮间隔点号乘2(i×2)逐次勾掉一些点。然后观察二个点时,三个点时,四个点时,以至更多一些点时,仍有对称点存在,所以即可推知n无论为多么大的数时仍有对称点存在。
也许有人不承不认这种证明,或者不满意这种证明。那么是否能找到一种具有数学表现形式的证明呢?回答是肯定的。因限于本文篇幅和目的,具有数学表现形式的证明从略。
第四步:用预备定理(LP)证明(A′)命题。
在点的序列下一一对应着写上从3开始的奇数列,如图:

按(LP)中给定的规则勾掉一些点,然后把对应于被勾掉点的数也勾掉(见图示)。
根据我们构造的方法可知,两个序列是同构的。因为上面点的序列我们已经证明,当n≥2时有对称点存在,所以下面的奇数列也必有对称的奇数存在,而余下的奇数恰恰都是奇素数,即有对称的奇素数存在。于是就证明了命题(A′)。又因为A′ A,所以也就证明了哥德巴赫猜想。
或许有人要问:为什么余下的数都是奇素数呢?这个问题只要您把素数分布规律
和(LP)中的勾点规则联系起来,稍加思索,就会不言而喻了。
第四步的证明方法叫做演绎法,具体点儿说就是“三段论式的A格”。数学工作者
大都知道,莱布尼兹曾经说过,数学证明很多都是三段论式。但是为什么有的数学家或专家却不承认它呢?!但却也未敢断然否定,只是说:“能那么简单吗?!”然而,孰不知欧几里得对素数有无穷多个的证明不是更简单吗!
尽管以简御繁,出奇制胜成功的先例很多,但是对这个数学家苦思冥索了二百多年而至今却未能解决的哥德巴赫猜想若说能:“神奇化易”恐怕是“痴人说梦”或者是“海外奇谈”了吧?
有句名言说得好:“真理往往是非常朴素的,以致人们不想信它。”然而,一旦真理朴素到中学生都能认识的程度,那么任何谎言就会不攻自破了。
笔者才疏学浅,但愿得到名家和有识之士不吝指教。
1983.12.15
根据我们构造的方法可知,两个序列是同构的。因为上面点的序列我们已经证明,当n≥2时有对称点存在,所以下面的奇数列也必有对称的奇数存在,而余下的奇数恰恰都是奇素数,即有对称的奇素数存在。于是就证明了命题(A′)。又因为A′ A,所以也就证明了哥德巴赫猜想。
或许有人要问:为什么余下的数都是奇素数呢?这个问题只要您把素数分布规律
和(LP)中的勾点规则联系起来,稍加思索,就会不言而喻了。
第四步的证明方法叫做演绎法,具体点儿说就是“三段论式的A格”。数学工作者
大都知道,莱布尼兹曾经说过,数学证明很多都是三段论式。但是为什么有的数学家或专家却不承认它呢?!但却也未敢断然否定,只是说:“能那么简单吗?!”然而,孰不知欧几里得对素数有无穷多个的证明不是更简单吗!
尽管以简御繁,出奇制胜成功的先例很多,但是对这个数学家苦思冥索了二百多年而至今却未能解决的哥德巴赫猜想若说能:“神奇化易”恐怕是“痴人说梦”或者是“海外奇谈”了吧?
有句名言说得好:“真理往往是非常朴素的,以致人们不想信它。”然而,一旦真理朴素到中学生都能认识的程度,那么任何谎言就会不攻自破了。
笔者才疏学浅,但愿得到名家和有识之士不吝指教。
1983.12.15
主要参考文献:1.《哥德巴赫猜想》潘承洞、潘承彪著
2.《神奇妙算》华罗庚著
3.《逻辑与数学教学》寿望斗著
4.《科学发现-纵横淡》王梓坤著
作者简介:谷立煌1937年1月27日出生。1960年毕业于哈工大土木系。工作 单位:中国科学院黑龙江分院、哈市自来水公司、王常市建设局规划处工程师.主要科技成 果是对三道数学难题(哥德巴赫猜想、费马大定理、比尔猜想)的证明,已先后发表在相关 刊物。2005年12月6日国家科技部基础司通知省科技厅对前两项成果上报“自然科学奖”。
通讯地址:五常市建设局 邮 编:150200
电 话:55070308
通讯地址:五常市建设局 邮 编:150200
电 话:55070308
附:





 京公网安备 11010602130025号
京公网安备 11010602130025号